Equipment Used:

thermistor interfaced to personal computer, thermometer, beaker of water and hot plate

Objectives:

1. to measure the temperature dependence of the resistance of a thermistor
2. to interpret the result in terms of the energy gap in the semiconductor material from which the thermistor is made

When a semiconducting solid crystal is formed from a collection of atoms, the interaction between the electrons and the periodic array of atoms produces a significant change in the states available to the less tightly bound electrons. These electrons are no longer bound to a single atom, but rather become "communal property’ of the whole solid, and they are able to move throughout the solid. For these electrons the energy states remain discrete, but the states group into bands. Within a band, the energies of the states are extremely close together, but between bands there is a comparatively large energy separation which is referred to as an energy gap. In a semiconductor the energy gap is of the order of 1 eV; at room temperature it is 0.67 eV for Ge (infrared radiation) and 3.6 eV for ZnS (far violet of visible spectrum).

In a manner similar to that for an atom, energy states in a solid are populated, starting with the lowest-energy level, in accordance with the Pauli exclusion principle. The band of highest energy states is called the conduction band, and the energy band just below it is called the valence band.

Absorption of energy by the semiconductor can boost electrons from the valence band to the conduction band, if the energy is at least as large as the energy gap. In the idealized situation of T = 0 K, the conduction band is completely empty. As the temperature is raised, some electrons get enough thermal energy to "pop up" into the conduction band, in accordance with statistical physics. In other words, higher energy states can be populated be electrons due to thermal excitation.

Electrical current consists of the movement of electric charge. Electrons in the conduction band are able to move from atom to atom, and so contribute to electric currents. An unoccupied state in the valence band is called a hole; electrons in the valence band can contribute to electric currents by moving to fill the hole states. When this happens it is easy to visualize a hole moving opposite the direction an electron moves in the valence band, and so this is referred to as hole conduction.

If the number of unoccupied states in the valence band equals the number of occupied states in the conduction band, the semiconductor is said to be intrinsic. For such a material it makes sense that the higher the temperature, the more charges (electrons in the conduction band and holes in the valence band) are available to move through the solid.

Therefore the electrical resistance would fall as the temperature of the semiconductor rises. The relationship turns out to be exponential, as suggested by a graph of the logarithm of resistivity versus the reciprocal of the temperature for a variety of intrinsic semiconductors. (Note that values of 1/T = 2 X 10^-3 and 1/T = 3 X 10^-3 respectively represent temperatures of 500 K and 333 K.)

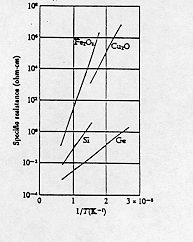
The linear relationship between the logarithm of resistivity and the reciprocal of the Kelvin temperature tells us that resistance R (which is proportional to resistivity) can be written as a function of temperature

where A and B are constants that can be obtained from the data. The constant A is the initial resistivity.

From the band theory of solids, it is deduced that the constant B is related to the energy gap E_g in an intrinsic semiconductor by

where k is Boltzmann's constant. Thus measurement of the resistance of a semiconductor as a function of temperature provides data from which the constant B and the energy gap can be determined.

You will measure the temperature dependence of the resistance of a thermistor, a device made from an intrinsic semiconductor. A thermistor is very useful as a device for measuring temperature because small changes in temperature produce rather large changes in its resistance. For example, the resistance of a commercial thermistor may change by an order of magnitude for a temperature change from 273 K to 373 K.

Procedure

You are provided with a commercial thermistor, which you can place in a beaker of water heated with a hot plate or other heating device. A thermometer allows you to monitor the temperature.

Measure the resistance of the thermistor from room temperature to 100°C. You are provided with a LABVIEW program which will prompt you to push a button when the temperature reaches a certain value. It will then record the corresponding voltage drop across the thermistor (which is proportional to its resistance). When the temperature has reached the boiling point, the computer will automatically save your data of temperature and voltage which you can export to a spreadsheet to analyze as described in the For Your Report section.

For Your Report

1) Create a spreadsheet into which you will import your data file for processing and graphing. Graph the logarithm of resistance versus 1/T.

   From equation (1) we get Equation (2):

2) Rearrange the above equation to prove that it doesn't matter what the units of R are, and that you may simply use the voltage, which is proportional to R. What does the slope of the graph give you?

3) From a regression fit of a straight line to your measured values of ln(R) versus 1/T, obtain your measured value of the energy gap E_g. Also obtain an estimate of the uncertainty in your value for E_g from the uncertainty in the slope of your fitted line. Express E_g and the uncertainty in eV.

(You'll need to know that k = 8.617 X 10^-5 eV/K.)

Is your value for E_g reasonable, given that for many semiconductors near room temperature the gap energy is on the order of 1 eV?

3) What are some of the possible sources of error in this experiment AND how would they affect the slope of your data? Is this what you see with your data?

References:

John R. Taylor and Chris D. Zafiratos, Modern Physics for Scientists and Engineers, Prentice-Hall (1991), pp. 513-519.

Robert A. Levy, Principles of Solid State Physics, Acadenic (1968), pp. 381ff.